J언어 배우기 - 제 3장: 함수 정의하기
Roger Stokes이 쓴 Learning J 의 chapter 3:Defining Functions를 번역/정리했다. 이전 챕터들은 본 사이트에서 J언어 태그로 검색해 볼 수 있다.
J에는 많은 내장 함수가 있다. 우리는 그 중 몇 가지를 살펴보았다.(*나 +같은 것들) 이번 섹션에서는 이 내장함수를 조합해 원하는 함수를 정의하는 여러 방법을 배운다.
3.1 이름짓기
함수를 정의하는 가장 간단한 방법은 그냥 원하는 내장 함수에 이름을 부여하는 것이다. 정의는 할당 함수를 이용해서 한다. 예를 들어서 아래의 square함수는 내장 함수인 *:를 이용하는 것과 똑같다.
square =: *:
square 1 2 3 4
1 4 9 16
우리가 지은 이름이 더 기억하기 쉽거나 해서 그게 좋다면 새로운 이름을 사용한다. 같은 내장 함수에 다른 두 개의 이름을 부여할 수도 있다. 하나는 모나딕용으로, 다른 하나는 다이아딕 용으로.
Ceiling =: >.
Max =: >.
| Ceiling 1.7 | 3 Max 4 |
| 2 | 4 |
3.2 삽입하기
표현식 +/ 2 3 4는 의미가 2 + 3 + 4와 같고 비슷하게 */ 2 3 4는 2 * 3 * 4와 같다. 이제 이 함수에 sum이라는 이름을 붙여보자.
sum =: + /
sum 2 3 4
9
sum =: +/라는 코드를 보면 +/가 이 자체로 함수를 표현하는 표현식임을 알 수 있다.
+/는 "Insert"(/)가 함수 +에 적용되어 리스트를 합치는 함수가 되었다 라고 말한다.
즉, /은 그 자체로 함수의 한 종류이다. 이 함수는 왼쪽에 인자 하나를 받는다. 그 인자도 함수고 계산 결과도 함수다.
3.3 용어: 동사, 연산자, 부사
우리는 두 종류의 함수를 봤다. 첫째로 "일반적인" 함수다. 숫자를 계산해서 숫자를 내뱉는 +나 *같은 함수. J에서는 이런 것들을 "동사"라고 한다. 둘째로 함수를 계산해서 함수를 내뱉는 /같은 함수이다. 이런 종류의 함수를 다른 종류의 함수와는 구별하여 "연산자"라고 한다.
하나의 인자를 받는 연산자는 "부사"라고 한다. 부사는 항상 왼쪽에 하나의 인자를 받는다. 그래서 표현식 + /에서 부사 /는 동사 +에 적용되어서 리스트를 더하는 동사가 만들어진다.
용어는 영어구문에서 따왔다. 동사는 물건의 행동을 묘사하고 부사는 동사의 의미를 변한다.
3.4 교환하기(Commuting)
부사 /말고 다른것도 보자. 부사 ~는 왼쪽과 오른쪽의 인자를 서로 바꾸는 기능이 있다.
| 'a' , 'b' | 'a' ,~ 'b' |
| ab | ba |
다이아드 함수 f와 그 인자 x, y에 대해서 ~의 구조는 다음과 같다.
x f~ y 는 y f x 이다
또 다른 예로 동사 |를 기억하는가? 2|7은 "7 mod 2"와 같다. 이제 mod함수를 정의 할 차례이다.
mod =: | ~
| 7 mod 2 | 2 | 7 |
| 1 | 1 |
그림을 한번 그려보자. 우선 함수 f에 인자 y를 적용해 f y의 결과를 반환하는 다이어그램이 있다. 이 다이어그램에서 함수 f는 사각형으로 그리고 인자가 어떻게 흘러서 결과가 나타나는지 화살표로 나타낸다. 각각의 화살표에는 표현식이 쓰여있다.
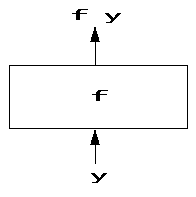
아래에 다이아딕 함수 f에 인자 x, y를 적용해 x f y가 만들어지는 다이어그램이 있다.
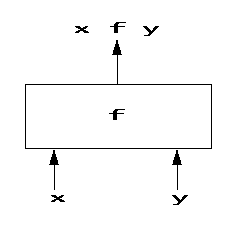
이것이 함수 f~에 대한 다이어그램이다. 상자 안에 함수 f가 있고 인자가 서로 엇갈려서 들어가는 그림으로 나타냈다.
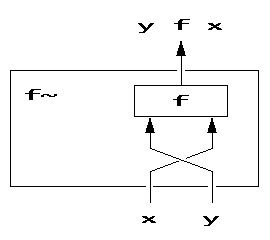
3.5 묶기(Bonding)
double이라는 동사를 정의해야한다고 가정해보자. double x는 x * 2를 뜻한다. 즉 double은 "곱하기 2"이다. 아래와 같이 정의할 수 있다.
double =: * & 2
double 3
6
우리는 *를 두 인자중 한 인자를 미리 정해놓고(이 경우엔 2) 그걸 마치 모나드 처럼 써서 *를 다이아드로 사용했다. & 연산자는 함수와 값을 묶어놓는 역할을 한다. f가 다이아딕 함수이고 k가 f의 오른쪽 인자라면 다음과 같은 구조를 가진다.
(f & k) y 은 y f k 이다.
오른쪽 인자말고 왼쪽 인자를 고정하고 싶다면 아래와 같이 쓸 수 있다.
(k & f) y 은 k f y 이다
예를 들어서 물건 값의 10% 세금은 계산해야 한다고 하자. 그러면 세액을 계산하는 함수는 다음과 같다.
tax =: 0.10 & *
tax 50
5
아래에 k&f함수의 다이어그램이 있다.
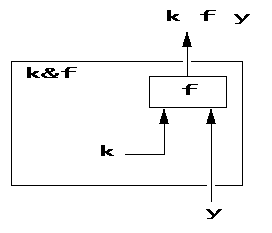
3.6 용어: 접속사와 동사
표현식 *&2는 & 연산자는 두 인자(동사 *와 숫자 2)를 받는 함수이며 그 결과로 "doubling"이라는 동사를 만들어낸다.
&와 같은 두 인자를 취하는 "연산자"를 J에서는 "접속사"라고 한다. 이는 두 인자를 묶어주기 때문이다. 반면에 부사는 하나의 인자만을 가지는 연산자이다.
J의 모든 함수는 내장 함수이건 사용자 정의 함수이건 반드시 4종류 중 하나이다. 모나딕 동사, 다이아딕 동사, 부사, 접속사가 그것이다. 같은 심볼이지만 다른 의미를 가지는 동사는 두 개의 다른 동사로 간주한다. 예를 들면 -는 모나딕으로는 "negation"이고 다이아딕으로는 "subtraction"이다.
J의 모든 표현식은 어떤 타입을 가진 값이다. 그리고 함수가 아닌 모든 값은 데이터이다.(정확히는 이전 섹션에서 본 배열이다)
J에서 데이터 값, 즉 배열은 "명사"라고 부른다. 이는 영어의 구문과 비슷하다. 이젠 어떤 것이 동사가 아닌 것을 강조하기 위해서 그것을 명사라 부르고, 어떤 차원을 가지고 있다는걸 강조하기 위해서 그것을 배열이라 부른다.
3.7 함수의 합성(composition)
이런 영어 표현을 생각해보자. "the sum of the squares of the numbers 1 2 3" 이건 1+4+9 또는 14이다. 우리가 앞에서 sum과 square동사를 정의 했으니 J로는 다음과 같이 쓸 수 있다.
sum square 1 2 3
14
sum과 square를 합성하여 하나의 "sum-of-the-squares"함수를 만들 수도 있다.
sumsq =: sum @: square
sumsq 1 2 3
14
심볼 @:(at colon)은 "composition(합성)" 연산자다. f와 g가 동사이고 y라는 인자가 있을때 이 연산자의 구조는 다음과 같다.
(f @: g) y 는 f (g y) 이다.
아래에는 이 구조에 대한 다이어그램이다.
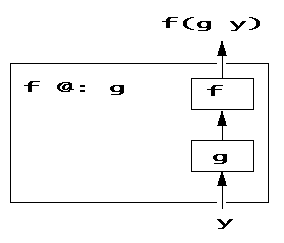
이 시점에서 독자분들은 동사를 합성할 때 왜 간단하게 f g라고 쓰지 않고 f @: g라고 쓰는지 궁금할 것이다. 간단히 말하자면 f g은 또 다른 의미이다. 이건 곧 나온다.
합성에 대한 다른 예는 화씨를 섭씨로 바꾸는 것이다. 32를 빼는 함수 s와 5%9를 곱하는 함수 m을 합성해보자.
s =: - & 32
m =: * & (5%9)
convert =: m @: s
| s 212 | m s 212 | convert 212 |
| 180 | 100 | 100 |
이 예제는 이름있는 함수의 합성을 잘 보여준다. 다음과 같이 함수의 표현식 자체를 합성 할 수도 있다.
conv =: (* & (5%9)) @: (- & 32)
conv 212
100
합성한 함수에 이름을 주지 않고서도 인자를 적용시켜 사용할 수 있다.
(* & (5%9)) @: (- & 32) 212
100
위 예제들로 모나드와 모나드를 합성한 것을 보였다. 다음 예제는 다이아드를 합성한 것이다. 일반적인 구조는 다음과 같다.
x (f @: g) y 은 f (x g y) 이다.
예를 들어서 아이템 몇 개를 구매한 총 금액은 각 아이템의 가격에 개 수를 곱하고 곱한 값을 더하면 알 수 있다. 아래를 보자.
P =: 2 3 NB. 가격
Q =: 1 100 NB. 개 수
total =: sum @: *
| P | Q | PQ | sum P Q | P total Q |
| 2 3 | 1 100 | 2 300 | 302 | 302 |
합성에 대해서 더 알고 싶으면 8장을 보라.
3.8 동사의 연결(Trains of Verbs)
"no pain, no gain"이라는 문구를 아는가. 이것은 압축되고 요약된 관용적 표현이다. 이런 말은 문법적 구조에는 맞지 않지만 제법 알아들을 수 있다. (메인 동사가 없으므로 문장이 아니다) J에는 이와 비슷하게 함수를 몇 개 연결해서 특정한 의미가 되도록 하는 표기법이 있다. 아래에 그 방법이 나온다.
3.8.1 훅(Hooks)
위에서 정의했던 세금을 계산하는 동사를 다시 가져오자. 이 동사에서 세율은 10%였다.
tax =: 0.10 & *
지불해야 하는 금액은 물건 가격 더하기 세금이다. 지불해야 하는 금액을 계산하는 동사는 다음과 같이 작성 할 수 있다.
payable =: + tax
만약 물건 가격이 50달러 라면, 아래와 같이 계산할 수 있다.
| tax 50 | 50 + tax 50 | payable 50 |
| 5 | 55 | 55 |
payable =: + tax라는 정의를 보면 +동사 다음에 곧바로 tax가 온다. 이 시퀀스는 할당 연산자 오른쪽에 위치함으로써 분리되어있다.(isolated) 이렇게 분리된 동사의 시퀀스를 "train"이라고 부르고 동사 2개의 train을 "hook"(훅)이라고 부른다.
두 개의 동사를 괄호 안에 넣어 분리시켜 훅의 형태로 사용할 수 있다.
(+ tax) 50
55
f가 다이아드, g가 모나드이고 y라는 어떤 인자가 있을때 훅의 일반적인 구조는 다음과 같다.
(f g) y 는 y f (g y) 이다.
이 구조를 다이어그램으로 나타내면 다음과 같다.
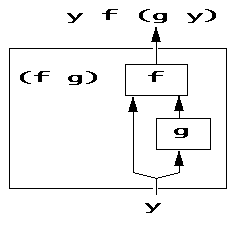
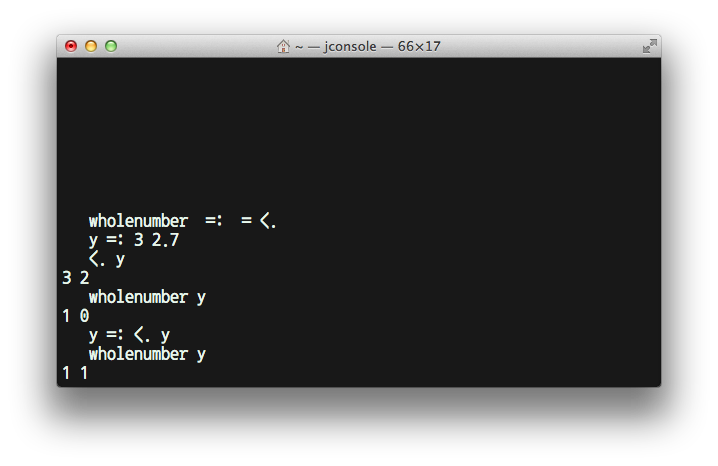
또다른 예로 인자로 들어온 수의 정수 부분을 계산하는 동사인 <.("floor")를 이용해보자. 숫자가 정수인지 아닌지 검사를 하려면 그 숫자가 정수부와 같은지 검사한다. "equal-to-its-floor"라는 의미를 가진 이 동사는 = <.라는 훅으로 정의할 수 있다.
wholenumber =: = <.
| y =: 3 2.7 | <. y | y = <. y | wholenumber y |
| 3 2.7 | 3 2 | 1 0 | 1 0 |
3.8.2 포크(Forks)
숫자 리스트 L의 산술 평균은 L의 합을 L의 아이템 개 수로 나눈 것이다.(아이템 개 수를 세는 모나딕 동사인 #는 기억하고 있겠지?)
| L =: 3 5 7 9 | sum L | # L | (sum L) % (# L) |
| 3 5 7 9 | 24 | 4 | 6 |
합을 아이템 개 수로 나누기 계산을 하는 동사는 세가지 동사의 시퀀스로 나타낼 수 있다. sum 다음에 %다음에 #가 오면 된다.
mean =: sum % #
mean L
6
세 동사의 분리된 시퀀스는 "fork(포크)"라고 한다. 임의의 인자 y에 대해서 f가 모나드이고 g가 다이아드이고 h가 모나드일 때 다음과 같은 일반적인 구조를 지닌다.
(f g h) y 는 (f y) g (h y) 이다.
이 구조를 다이어그램으로 나타내면 아래와 같다.

포크에 대한 다른 예로는 숫자 리스트의 범위를 구하는 것이 있다. 숫자 리스트의 범위는 리스트에서 가장 작은 수와 가장 큰 수를 구하는 것이다. 이는 최소, 최대를 구하는 동사 중간에 콤마 동사를 넣어 포크하면 된다.
리스트에서 가장 큰 수를 구하는 함수 >./와 가장 작은 수를 구하는 함수 <./는 1장에서 배웠다.
range =: <./ , >./
| L | range L |
| 3 5 7 9 | 3 9 |
훅과 포크는 동사의 시퀀스이다. 이는 동사의 "trains" 라고도 말한다. trains에 대해 더 많은 정보를 알려면 제 9장을 참고하라.
3.9 다 집어넣고 보자(Putting Things Together)
이제까지 배운 것들 중 몇가지를 섞어서 좀 더 커다란 예제를 만들어보자 어떤걸 만들꺼냐면, 숫자 리스트를 보여주고 각 숫자가 전체에서 몇 퍼센트를 차지하는지 보여주는 간단한 표를 만들 예정이다.
어떤걸 만들어야 하는지 명확히 하기 위해 우선 완성된 예제를 먼저 보자. 아래에 설명 할 것이기 때문에 당장에 이 모든걸 알 필요는 없다. 그냥 아래 6라인의 코드를 보고 어떤 동사가 정의되어 있는지 살펴보자.
percent =: (100 & *) @: (% +/)
round =: <. @: (+&0.5)
comp =: round @: percent
br =: ,. ; (,. @: comp)
tr =: ('Data';'Percentages') & ,
display =: (2 2 & $) @: tr @: br
간단한 데이터로 시작해보자.
data =: 3 5
이 데이터를 이용하면 display동사는 각 숫자와 그 숫자의 퍼센트를 표현할 것이다. 아래 표를 보자면, 3은 8에서 38%를 차지한다.
display data
+----+-----------+
|Data|Percentages|
+----+-----------+
|3 |38 |
|5 |63 |
+----+-----------+
percent동사는 훅 % +/으로 전체 수에서 각각의 수를 나누고 각각에 100을 곱해서 퍼센트를 계산해낸다. 아래에 percent의 정의를 다시 쓸테니 위로 스크롤 하지 않아도 된다.
percent =: (100 & *) @: (% +/)
이를 사용해보자.
| data | +/ data | data % +/ data | (% +/) data | percent data |
| 3 5 | 8 | 0.375 0.625 | 0.375 0.625 | 37.5 62.5 |
퍼센트 값을 반올림하자. 반올림은 각 값에 0.5를 더하고 "floor"(<.)를 이용해 정수 부분만을 취한다. 이런 일을 하는 동사 round는 아래와 같이 정의한다.
round =: <. @: (+&0.5)
그러면 화면에 표시할 값을 계산하는 동사는 다음과 같다.
comp =: round @: percent
| data | comp data |
| 3 5 | 38 63 |
이제 테이블에 데이터와 퍼센트로 계산된 값을 표현해야 한다. 리스트를 하나의 열(column)을 만들기 위해선 동사 ,.를 사용할 수 있다.("Ravel Items"라고 부른다)
| data | ,. data | ,. comp data |
| 3 5 | 3 5 |
38 63 |
테이블의 아래쪽 행을 만들기 위해 br 이라는 동사를 정의한다. 이 동사는 데이타와 계산된 값을 열(column)로 링크하는 포크이다.(포크는 위에서 정의했듯이 세 동사의 시퀀스이다.)
br =: ,. ; (,. @: comp)
| data | br data |
| 3 5 | +-+--+ |3|38| |5|63| +-+--+ |
테이블의 위쪽 행(컬럼 헤딩)은 간단하게 만들 수 있다. 아래쪽 행은 두 박스의 리스트이다. 우리가 그 앞에 두 개의 박스를 더 붙이면 박스가 4개인 리스트가 된다. 동사 tr이 그 작업을 한다.
tr =: ('Data';'Percentages') & ,
| data | br data | tr br data |
| 3 5 | +-+--+ |3|38| |5|63| +-+--+ |
+----+-----------+-+--+ |Data|Percentages|3|38| | | |5|63| +----+-----------+-+--+ |
남은건 박스 4개의 리스트를 2행 2열의 테이블로 만드는 것이다.
(2 2 & $) tr br data
+----+-----------+
|Data|Percentages|
+----+-----------+
|3 |38 |
|5 |63 |
+----+-----------+
이걸 다 합하면,
display =: (2 2 & $) @: tr @: br
display data
+----+-----------+
|Data|Percentages|
+----+-----------+
|3 |38 |
|5 |63 |
+----+-----------+
이렇게 된다.
display동사는 두 부분으로 나눈다. 반올림된 퍼센트 값을 계산하는 comp함수와 화면에 결과를 표시하는 나머지 부분이 그것이다. comp함수를 바꾸어 다른 함수를 사용하면 그 함수의 계산 결과를 표 형태로 표시한다. comp를 제곱근을 계산하는 %:함수로 바꿔보자.
comp =: %:
동사 tr에 있는 표의 컬럼 헤딩도 알맞게 수정해야한다.
tr =: ('Numbers';'Square Roots') & ,
display 1 4 9 16
+-------+------------+
|Numbers|Square Roots|
+-------+------------+
| 1 |1 |
| 4 |2 |
| 9 |3 |
|16 |4 |
+-------+------------+
J의 몇몇 특징적인 기능(묶기, 합성, 훅, 포크)을 이용해서 조그마한 J프로그램을 작성해보았다. 모든 J 프로그램과 마찬가지로 이 프로그램은 이걸 작성하는 많은 방법중에 하나일 뿐이다. 이 장에서 우리는 함수를 정의하는 방법을 배웠다. 함수는 두 종류가 있다. 동사와 연산자. 지금까지 우리는 동사의 정의하는 것을 보았다. 다음 장에서는 동사를 정의하는 다른 방법을 알아 볼 것이다. 그리고 제 13장에서는 연산자를 정의하는 방법을 배운다.
이렇게 제 3장이 끝났다.